Tweet-Toot: Building a bot for Mastodon using Python
The Mastodon social network has been steadily gaining popularity over the last several years. One of the main reasons for this is that Mastodon is a decentralised social network, which means that it doesn’t have a central authority or corporation that governs how you use it. When you signup on a Mastodon “instance”, you become part of your own little community with its own rules and code of conduct, and many such instances connect to form a larger Mastodon network. There are instances devoted to technology, arts and sciences, gaming, and even cat memes, and all of these connect with each other and become part of a larger whole.
This open, community-centric approach means that you can belong to the community where you feel most comfortable, and still interact with the rest of the world from the comfort and security of your own instance. Add to this the fact that each instance is managed by a human administrator that you can reach whenever you want, Mastodon is now what social networks were supposed to be from the start: “social” “networks”.
So, what is a bot and why do I need it?
A “bot” is very simple a script that runs automatically and performs a particular task. For example, a simple script could monitor an account on twitter and repost new tweets on Mastodon, or it could watch our favourite websites and post content to our instance whenever they have new content. These are just two examples of how we can use the API to make our community richer and more exciting 🙂.
Getting Started
Let’s pick a twitter account to automatically cross-post to Mastodon whenever there is new content. There’s one called Mother of Sarcasm. Here’s a sample:
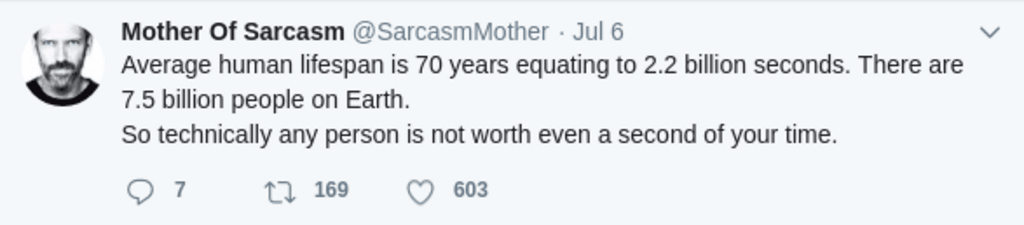
The goal we want to achieve is this: we want to create a Python script that will run as a scheduled job, get any new tweets the above account posts, and then post them to a Mastodon instance of our choice. This task would require the following:
- We would need to create a new Mastodon account for our bot.
- Our script will need to pull tweets from the twitter account we’ve selected.
- The same script will check if the tweet is new, and then post it to our bot’s Mastodon account.
This simple 3-step process will allow use to build our twitter relay. I’ll be using Python 3 to write the script, but you can use any other programming language that you like. I’ll add some links to other SDKs at the bottom of these notes.
Registering a new bot account
First things first, we’ll need a new Mastodon account for our bot. We could just use our personal account for this, but creating a separate account for the bot has some advantages:
- If our bot misbehaves, our friendly neighbourhood instance admin can safely block our bot’s account, instead of blocking ours.
- Some instances have codes of conducts that don’t allow the use of bots.
- The botsin.space instance is dedicated to bots. So head over to the instance’s Mastodon page and sign-up for a new account.
Customising the bot’s profile
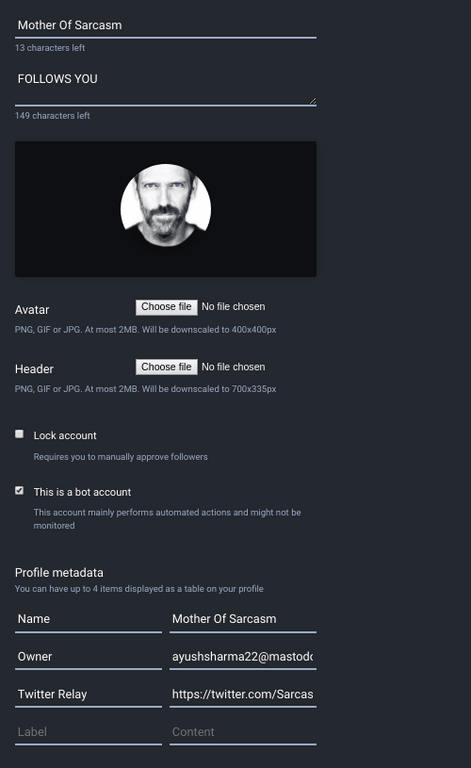
Once the account is created, it’s time to customise it. We want to make our bot’s profile look like the profile for the twitter account, so that fans of the original can find it more easily. This means updating the profile photo and bio of our bot account to match the twitter account. We also want to identify our bot more clearly so that people know they’re not talking to a real person.
Let’s update our bot account’s preferences with the following:
- The profile name and bio should match the one on the twitter account.
- The
This is a bot accountcheckbox should be checked. This will show aBotlabel under this profile. - In
Profile metadata, we’ll need anOwnerentry pointing to our personal Mastodon profile. This will allow instance admins to get in touch with us in case the bot misbehaves. It’s also a nice way to help other Mastodonians reach out if they have kudos, questions, or criticisms. - Let’s add another
Twitter Relayentry pointing to our chosen twitter account.
Once this is done, hit save, and behold the face of your new bot. Here’s what mine looks like:
Getting the developer access token for our script
With the profile customised, we now want to configure the access tokens for this account so we can access it from our Python script. To do this, we’ll need to create an Application for our new account.
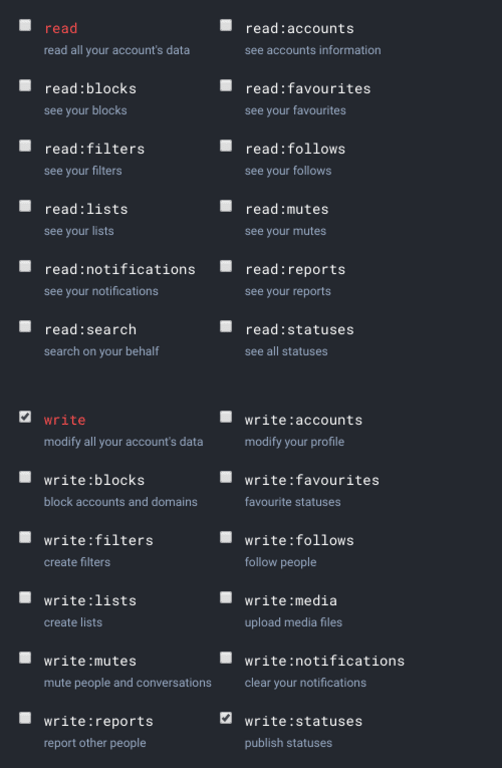
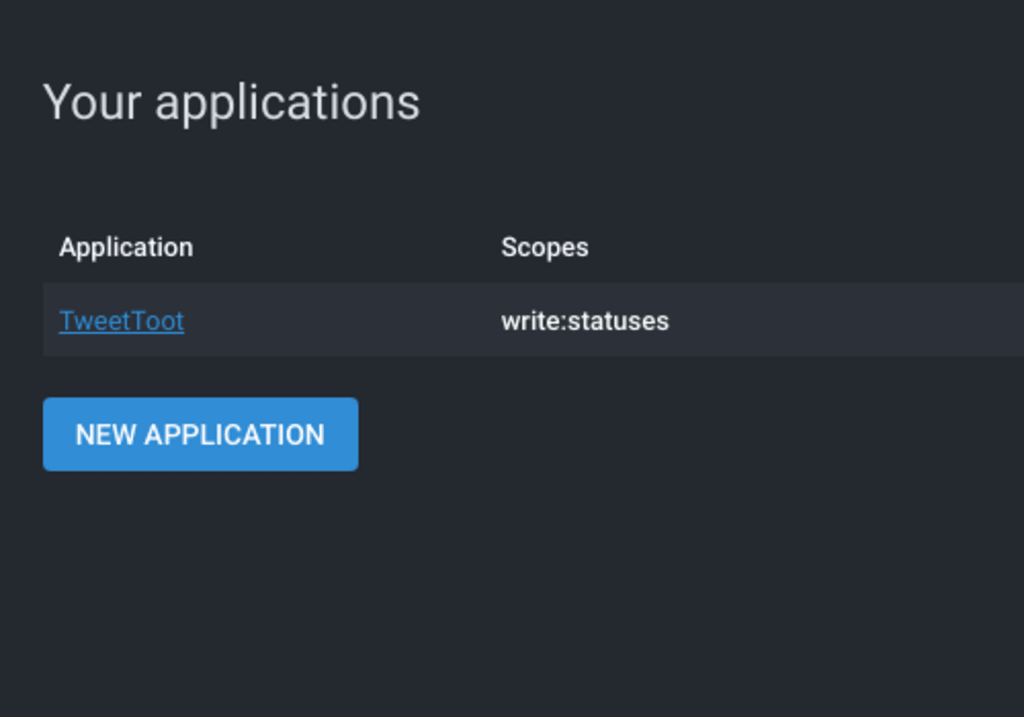
On the Preferences > Development page, click New Application:
- Give the application a name. I’ve chosen
TweetToot. - For permissions, enable the
write:statusespermission and nothing else. We only want our bot to toot.
Once the Application is created, we’ll be provided with access tokens that we can use to create our bot.
Please heed the warning: `Be very careful with this data. Never share it with anyone!”. If the credentials are compromised, anyone will be able to toot from this account. That is why its important that this application only have the minimum permissions it requires to operate.
Back on the Development screen, our new application will look like this:
Alright, let’s take a breath. So far we’ve accomplished the following:
- We’ve created a Mastodon account with a profile matching our chosen twitter account.
- We’ve marked our account as a bot, and provided contact information in case our bot malfunctions.
- We’ve created an Application for this bot, and restricted it to only post new toots.
- We’ve also created access credentials for the Application which we can use in our code.
Coding our new bot
I’ve uploaded the complete working code for this bot on GitLab. I’ll review the important sections here so you can reproduce it.
As I mentioned earlier, I’ve used Python 3 to build this bot. The two libraries we’ll need are beautifulsoup4 and requests. We can install these using:
pip3 install requests beautifulsoup4
With the requirements installed, we can add the two important functions our bot will need: fetching new tweets from twitter, and posting the new ones to Mastodon.
Fetching new tweets from twitter
Twitter has been cracking down on its API over the last few years to shutdown third-party clients, which means that we’ll need to scrape the twitter account page directly and extract the tweets from the HTML source itself. I should warn you that scraping is illegal, and you should find more legal alternatives if you can. For now I’m going to demonstrate the scraping option. To scrape the Mother of Sarcasm account and extract the tweets in Python 3, we would create a function like this:
def getTweets():
all_tweets = []
url = 'https://twitter.com/SarcasmMother'
data = requests.get(url)
html = BeautifulSoup(data.text, 'html.parser')
timeline = html.select('#timeline li.stream-item')
for tweet in timeline:
tweet_id = tweet['data-item-id']
tweet_text = tweet.select('p.tweet-text')[0].get_text()
all_tweets.append({"id": tweet_id, "text": tweet_text})
return all_tweets if len(all_tweets) > 0 else None
Here’s what the above function is doing:
- Use the
Requestslibrary to fetch the HTML of our twitter account’s main page. - Extract the HTML using the
Beautiful Souplibrary. - Extract all content with the tweet’s
litags and put them in a dictionary with its Tweet ID and content. - Add the above dictionary to a list so we can loop over it.
Once this function completes, it will return a Python list that will contain all our tweets with their tweet IDs and tweet content.
Posting new tweets to our bot’s Mastodon account
The above function will give us a Python list, where each item is itself a dictionary containing the unique ID of that tweet and the tweet content. The tweet ID is important because we’re going to use it to check if we’ve already sent this tweet before, and if so, we’ll ignore the tweet and move on to the next one.
The function to take a dictionary item returned in getTweets() above and then post it to Mastodon would look like this:
def tootTheTweet(tweet):
host_instance = 'https://botsin.space'
token = 'AAAAA-BBBBB-CCCCC-DDDDD-EEEEE'
headers = {}
headers['Authorization'] = 'Bearer ' + token
data = {}
data['status'] = tweet['text']
data['visibility'] = 'public'
response = requests.post(
url=host_instance + '/api/v1/statuses', data=data, headers=headers)
if response.status_code == 200:
return True
else:
return False
Our function above will post the tweet to Mastodon as follows:
We’re setting the access token we received earlier in the Authorization: Bearer token so that our Mastodon instance knows who we are.
We set the content and visibility in the parameters for our POST request.
We POST the request to the API endpoint of our chosen instance.
Running this code should give is a HTTP 200 response, meaning that everything went fine. The instance API will return some helpful response messages to let us know what happened, and we should be able to see our tweet on the bot’s profile page.
When you see the tweet posted as your Mastodon bot’s toot, you will have successfully created your Mastodon bot 🙂
The Complete Tweet-Toot
The full, working code for this bot can be found on GitLab.
Getting Tweet-Toot working is pretty easy. Before you can install it, you’re going to need to do the following:
- Clone this repository.
- Install the Python3 libraries
requestsandbeautifulsoupmentioned in therequirements.txtfile. - In
config.json, update the following:
tweets.source_account_url: The source Twitter account.toots.host_instance: The HTTPS URL of your instance.toots.app_secure_token: The Mastodon app access token.
For example:
tweets.source_account_url= https://twitter.com/SarcasmMothertoots.host_instance= https://botsin.spacetoots.app_secure_token= XXXXX-XXXXX-XXXXX-XXXXX-XXXXX’
Once this is all setup, you can run the bot like this:
python3 run.py
If all goes well, you’ll see something like this:
Tweet-Toot | 2018-08-20 21:21:52 _info > getTweets => Fetching tweets for https://twitter.com/SarcasmMother.
Tweet-Toot | 2018-08-20 21:21:52 _info > __main__ => 20 tweets fetched.
Tweet-Toot | 2018-08-20 21:21:52 _info > tootTheTweet => 1031383086963994625 already tooted. Skipping.
Tweet-Toot | 2018-08-20 21:21:52 _info > tootTheTweet => 1031382821791657984 already tooted. Skipping.
Tweet-Toot | 2018-08-20 21:21:53 _info > tootTheTweet => OK (Response: {"id":"100583362607805661","created_at":"2018-08-20T15:51:53.284Z","in_reply_to_id":null,"in_reply_to_account_id":null,"sensitive":false,"spoiler_text":"","visibility":"public","language":"en","uri":"https://botsin.space/users/motherofsarcasm/statuses/100583362607805661","content":"\u003cp\u003eYou are paid by how hard you are to replace. Not by how hard you work.\u003c/p\u003e","url":"https://botsin.space/@motherofsarcasm/100583362607805661","reblogs_count":0,"favourites_count":0,"favourited":false,"reblogged":false,"muted":false,"pinned":false,"reblog":null,"application":{"name":"TweetToot","website":""},"account":{"id":"12345","username":"motherofsarcasm","acct":"motherofsarcasm","display_name":"Mother Of Sarcasm","locked":false,"bot":true,"created_at":"2018-08-20T15:07:42.747Z","note":"\u003cp\u003eFOLLOWS YOU\u003c/p\u003e","url":"https://botsin.space/@motherofsarcasm","avatar":"https://files.botsin.space/accounts/avatars/000/058/348/original/658f78e1f07e94fa.jpg","avatar_static":"https://files.botsin.space/accounts/avatars/000/058/348/original/658f78e1f07e94fa.jpg","header":"https://botsin.space/headers/original/missing.png","header_static":"https://botsin.space/headers/original/missing.png","followers_count":0,"following_count":1,"statuses_count":3,"emojis":[],"fields":[{"name":"Name","value":"Mother Of Sarcasm"},{"name":"Owner","value":"ayushsharma22@mastodon.technology"},{"name":"Birdsite","value":"\u003ca href=\"https://twitter.com/SarcasmMother\" rel=\"me nofollow noopener\" target=\"_blank\"\u003e\u003cspan class=\"invisible\"\u003ehttps://\u003c/span\u003e\u003cspan class=\"\"\u003etwitter.com/SarcasmMother\u003c/span\u003e\u003cspan class=\"invisible\"\u003e\u003c/span\u003e\u003c/a\u003e"}]},"media_attachments":[],"mentions":[],"tags":[],"emojis":[]})
Tweet-Toot | 2018-08-20 21:21:53 _info > __main__ => Tooted "You are paid by how hard you are to replace. Not by how hard you work."
Tweet-Toot | 2018-08-20 21:21:53 _info > __main__ => Tooting less is tooting more. Sleeping...
Important considerations before deploying Tweet-Toot
With out bot working, there are a few things we need to talk about before we can deploy this bot to production.
Since our bot is going to be running as a cron job, it will pick up the same set of tweets a number of times from the twitter account until it finds new content. This means that we need a way to check if we’ve tooted a tweet to Mastodon already, otherwise we’ll end up posting every tweet to our Mastodon instance and toot-blast the server.
There are two things we can do: we can add a check in our script to ensure we only post a tweet once, and we can leverage a server-side Mastodon feature to ensure the same thing.
Checking for a tweet before duplicate posting
If you look at the tootTheTweet() method in the social.py file on the GitLab repo, you’ll see the following code:
tweet_check_file_path = helpers._config('toots.cache_path') + tweet['id']
tweet_check_file = Path(tweet_check_file_path)
if tweet_check_file.is_file():
helpers._info('tootTheTweet() => Tweet ' + tweet_id + ' was already posted. Skipping...')
return False
else:
tweet_check = open(tweet_check_file_path, 'w')
tweet_check.write(tweet['text'])
tweet_check.close()
helpers._info('tootTheTweet() => New tweet ' + tweet_id + ' => "' + tweet['text'] + '".')
If you look at the function lines above, we’ve implemented a check as follows:
Create a new file path by appending the tweet ID to any directory, say the /tmp directory.
Check if this file already exists. If it does, we’ve posted this tweet before, and we need to stop posting this one again.
If the file does not exist, create this file but continue posting the tweet. The next time this function executes, its going to find our check file and not tweet again.
If you look at the logs I posted above, you’ll notice two lines:
Tweet-Toot | 2018-08-20 21:21:52 _info > tootTheTweet => 1031383086963994625 already tooted. Skipping.
Tweet-Toot | 2018-08-20 21:21:52 _info > tootTheTweet => 1031382821791657984 already tooted. Skipping.
These lines are the output of the duplicate check we placed. Those two tweets were posted earlier, their check files were created, and so they weren’t posted again.
This is a very simple mechanism we can implement within our script to ensure we don’t post duplicate tweets.
Using Mastodon’s Idempotency-Key Check
Mastodon’s API also implements an idempotence check. The way it works is as follows: we add an Idempotency-Key header with a random value to every request we send. If we send another with the same value for that header, the request is rejected by Mastodon. So how can we use this to prevent duplicate toots?
In our tootTheTweet() function, let’s add one line:
headers['Idempotency-Key'] = tweet_id
This line will now send the tweet ID we extracted as the idempotence header value for this request. In the event our manual duplicate checking function fails, we’ll send the request for a duplicate toot with the same tweet ID as the original, which will cause the Mastodon API to reject it. This is a more reliable way to ensure duplicate toots don’t end up on Mastodon, but we should first try to remove duplicates ourselves rather than thrash the server and have it do our homework. This feature is easy to check: during testing, just remove manual file check and run your script multiple times. You’ll notice that only new toots end up on your bot’s profile.
So by implementing both these mechanisms, we can have our scripts check for duplicates and have the Mastodon API provide a strong failsafe as an idempotence check.
Closing Thoughts
This has been a long note, but by now your bot must be happily tooting 🎉. Just a few closing thoughts to keep in mind:
- The script is designed to toot once per invokation. I recommend timing your cron jobs according to the post frequency that you need instead of modifying the code.
- Mastodon instance admins are people too. Don’t toot-blast your instance and make life harder for them.
- When configuring your bot, ensure you clearly display an account where you can be reached in case of issues.
- When in doubt about some new code your write, have your code fail or
exit()first instead of doing something wrong.

&emoji=☕&slug=ayushsharma&button_colour=FFDD00&font_colour=000000&font_family=Cookie&outline_colour=000000&coffee_colour=ffffff)